by Nicolas Bonfante

Background

Polly

My GSoC project is part of Polly. Polly is a loop and data-locality optimizer for LLVM. The optimisations are made using a mathematical model called the polyhedral model. A key aspect of the model is the ability to reason about the memory access behavior in a very fine-granular way. This enables us to express very fine-granular way in a mathematical domain, where we deal with polyhedra instead of LLVM instructions. After modeling, transformations (tilling, loop fusion, loop unrolling …) can be applied on the model to improve data-locality and/or parallelization.

Some definitions are needed to understand this report.

Scop : Static COntrol Part. Sequences of loops that are optimizable by the polyhedral model.

ScopStatement : Statement in the Scop. Every statement represents a single basic block of LLVM-IR.

Memory Access : Happened every time the program interact with the memory, either by reading it or by writing to.

ScopArrayInfo : A data structure in Polly that store information about arrays in the SCoP.

ISL

ISL is the Integer Set Library used in Polly to handle all the mathematical computation during modelling and transformation. A basic understanding of what is ISL and how to use it is necessary to understand the implementation part of this report.

Data structures

ISL has different types of data structures.

• Set : A set in ISL is represented as follow :

\[\{ S[i_0, ..., i_n] : c_0, ..., c_n\}\]

Where $i_k$ is an input variable and $c_k$ is a constraint.

For example, the set of all instances of the statement S of the following code source is ${ S[i, j] : i=j, 0 \le i \le N, 0 \le j \le N}$.

for (int i = 0; i < N; i++)
  for (int j = 0; j < N; j++)
    if (i == j)
S:    A[i][j+1] = i*j;

• Union Set : An union set is just an union of sets.

• Map : A map in ISL represents a relation. It is represented as follows:

\[\{ S[i_0, ..., i_n] \rightarrow T[o_0, ..., o_n] : c_0, ..., c_n\}\]

Where $i_k$ is an input variable, $o_k$ is an output variable and $c_k$ is a constraint. For example, to model the memory access inside the statement S of the preeceding example, the corresponding map is :

\[\{ S[i, j] \rightarrow A[i, j+1] : i=j, 0 \le i \le N, 0 \le j \le N \}\]

This map means that in the statement S, there is a memory access to the array A at the indices [i, j+1].

BE CAREFUL : there is implicit constraints in this map. An unsimplified version of this map is :

\[\{ S[i_0, i_1] \rightarrow A[o_0, o_1] : i_0=i_1, i_0=o_0, i_1=o_1-1\}\]

The input part of the map is called the domain whereas the output part is called the range. For example, the domain and the range of the previous map are :

\(domain(\{ S[i, j] \rightarrow A[i, j+1] : i=j\}) = \{ S[i, j] : i=j\}\) \(range(\{ S[i, j] \rightarrow A[i, j+1] : i=j\}) = \{ A[i, j+1] : i=j\}\)

• Union Map : An union map is just an union of map.

• Nested Map : There is a specific type of map called nested map. The structure is the following :

\[\{ [ S[i_0, ..., i_n] \rightarrow T[j_0, ..., j_m] ] \rightarrow [ U[k_0, ..., k_r] \rightarrow V[l_0, ..., l_t] ] : c_0, ... , c_a\}\]

With this kind of data structure, we can represent data dependencies. Let take an example.

for (int i = 0; i < N; i++) {
   for (int j = 0; j < N; j++) {
S:   B[i][j] = i*j;;
   }
T: A[i] = B[0][i];
}

There is a RAW dependency for the array B because we read index i of B in statement T after that the statement S has written to index j of B. The dependences map looks like :

\[\{ [ T[i] \rightarrow B[0, i] ] \rightarrow [ S[i, j] \rightarrow B[i, i] ] : 0 \le i \le N, 0 \le j \le N \}\]

Maximal Static Expansion

Data-dependences in a program can lead to a very bad automatic parallelization. Modern compilers use techniques to reduce the number of such dependences. One of them is Maximal Static Expansion. The MSE is a transformation which expand the memory access to and from Array or Scalar. The goal is to disambiguate memory accesses by assigning different memory locations to non-conflicting writes. This method is described in a paper written by Denis Barthou, Albert Cohen and Jean- Francois Collard.1 Let take a example (from the article) to understand the principle :

int tmp;
for (int i = 0; i < N; i++) {
    tmp = i;
    for (int j = 0; j < N; j++) {
        tmp = tmp + i + j;
    }
    A[i] = tmp;
}

The data-dependences induced by tmp make the two loops unparallelizable : the iteration j of the inner-loop needs value from the previous iteration and it is impossible to parrallelize the i-loop because tmp is used in all iterations. If we expand the accesses to tmp according to the outermost loop, we can then parallelize the i-loop.

int tmp_exp[N];
for (int i = 0; i < N; i++) {
    tmp_exp[i] = i;
    for (int j = 0; j < N; j++) {
        tmp_exp[i] = tmp_exp[i] + i + j;
    }
    A[i] = tmp_exp[i];
}

The accesses to tmp are now made to/from a different location for each iteration of the i-loop. It is then possible to execute the different iteration on different computation units (GPU, CPU …).

Static Single Assignement

Due to lack of time, I was not able to implement maximal static expansion but only fully-indexed expansion. The principle of fully-index expansion is that each write goes to a different memory location. Let see the idea on an example :

int tmp;
for (int i = 0; i < N; i++) {
    tmp = i;
    for (int j = 0; j < N; j++) {
        B[j] = tmp + 3;
    }
    A[i] = B[i];
}

For the sake of simplicity, only the arrays will be expanded in this example. The fully expanded version is :

int tmp;
for (int i = 0; i < N; i++) {
    tmp = i;
    for (int j = 0; j < N; j++) {
        B_exp[i][j] = tmp + 3;
    }
    A_exp[i] = B_exp[i][i];
}

The details of fully-indexed expansion will be discussed in the following sections.

My contributions

My project is part of Polly. I am a french student but during the GSoC I was a student at the university of Passau, Germany. The LooPo team welcomes me and more especially Andreas Simbürger, one of my GSoC mentor. My other GSoC mentor is Michael Kruse, one of the main contributor to Polly, actually working in France. I’d like to thank all the people that help and guide me and more especially Andreas and Michael.

JSON Importer: Robustness improvement

As first step in open source software development and to get familiar with Polly/LLVM development process, I fixed an open bug in Polly. Polly can import data from a JSON file (in case of Polly called jscop file). From this JSON file it is possible to alter the existing modelling of a SCoP and even trigger code generation for new array accesses. This interface is mainly used for debugging and testing and therefore lacked a lot of consistency checks. This often triggered errors in the remaining part of the Polly optimization pipeline. My first step was, therefore, to implement those missing checks.

The resulting commit can be found here:

https://reviews.llvm.org/D32739

This patch has been merged into Polly.

Allocate arrays on the heap

Polly was already able to generate necessary array creation code, if that array has to be located on the stack as part of the pattern-based optimization of matrix multiplication. However, array allocation on the heap, which provides the amount of memory needed for full static array expansion was not possible before. Consider the following code as an example:

for (int i = 0; i < N; i++)
  for (int j = 0; j < N; j++)
    for (int k = 0; k < N; k++)
      for (int l = 0; l < N; l++)
        A[l] = 3;

The expansion would lead to the following code :

for (int i = 0; i < N; i++)
  for (int j = 0; j < N; j++)
    for (int k = 0; k < N; k++)
      for (int l = 0; l < N; l++)
        A_exp[i][j][k][l] = 3;

Depending on the value of N, A_exp can have a huge number of elements. If N = 100, we have $100100100*100 = 100000000 = 10^8$ elements ! Thus, the possibility to allocate array on heap was needed.

On the implementation side, special care had to be taken to get the memory allocation/deallocation correct. As opposed to stack-arrays which get freed automatically, heap allocated arrays require explicit calls to malloc and free. As Polly already guards the code that is generated during the execution of its’ optimization pipeline behind a branch, we have chosen to specifically create BasicBlocks right after the branch and right before the join to place our calls to malloc and free for any array that needed to be created on the heap. As an incremental step, this could be tested via the JSON Importer. We concluded to this sollution after long discussion with the Polly community to ensure that we do not risk a use after free error with the newly added arrays.

The finished support for heap allocation was committed into Polly and all discussion about it can be found here:

https://reviews.llvm.org/D33688

Maximal Static Expansion

Maximal refers to a static expansion that requires the least amount of memory. As before, we have chosen an iterative approach to implement this. With the heap allocation and stable testing support in the JSONImporter in place, we proceed to implementing just any expansion and continue with the implementation of the maximal one. This ensures that we first focus on the correctness of the basic expansion. This will already provide us the elimination of all but true dependencies (also known as flow dependencies). Any optimization we apply afterwards will provide us with less space requirement and, therefore, only expand the useability in terms of memory consumption.

Fully-Indexed Static Expansion

This will describe the most simple form of static expansion. From all possible memory access types (Scalars, Arrays, PHI) we have started with an implementation that supports the expansion of only arrays, because we only have to convert one array to another one. As a basic property of static expansion we have one single write per array cell. We ensure this by transforming each write-access into a new array (located on the heap). Afterwards, we have to remap all read accesses to the old write-access to the correct new array and the correct new array index (based on polyhedral dependecy information). Naturally we would resort to statement-level dependencies, which map statement instances (i.e., “S[i][j]” in the example below) to statement- instances. However, due to the coarse granularity of polly (i.e., one BasicBlock forms one statement), we are forced to use reference-based dependencies. These give us the possibility to filter all dependencies for only the one array access that we are interested in for the expansion.

The basic implementation of our Fully-Indexed Static Expansion was committed to Polly and can be found here:

https://reviews.llvm.org/D34982

The switch from Statement-Level to Reference-Level dependencies can be found here:

https://reviews.llvm.org/D36791

Finally, the expansion to Scalars and PHI nodes was committed as well and can be found here:

https://reviews.llvm.org/D36647

Support for Scalars and PHI nodes

Inside Polly one encounters scalar values of two kinds. First, the standard scalar value, which is just a single value (MemoryKind::Value). Second, a PHI node (MemoryKind::PHI). These virtual nodes are represented in Polly as scalar values that are read at the definition of the PHI node, and written at the end of every source BasicBlock. Let us consider the following example:

int tmp = 0;
for (int i = 0; i < N; i++) {
    tmp = tmp + 2;
}

In LLVM, everything is transformed in SSA. This means that Polly sees the following source code :

int tmp = 0;
for (int i = 0; i < N; i++) {
    tmp_1 = PHI(tmp, tmp_2)
    tmp_2 = tmp_1 + 2;
}

$tmp_1$ has not always the same source depending on the iteration the i-loop is in. If i=0, the source is tmp otherwise the source is tmp_2 of the previous iteration.

The expansion of the scalar write access is trivial because it behaves similar to the array case. PHI nodes have to be treated a little bit different to normal memory accesses. Due to their nature of (guaranteed) one read and possibly multiple writes we can switch the roles and perform the same expansion as in the case of normal scalar values.

Example

int tmp;
for (int i = 0; i < N; i++) {
    tmp = i;
    for (int j = 0; j < N; j++) {
S:      B[j] = tmp + 3;
    }
T:  A[i] = B[i];
}

The write to B occurs inside the i and j loops. Therefore, the expanded version of B must be a two-dimensional array indexed by i and j. The write to A occurs inside the i loop only, therefore it would no need expansion. But for the sake of simplicity, we still create an expanded version of A. After write expansion, the code would look as follows:

int tmp;
for (int i = 0; i < N; i++) {
    tmp = i;
    for (int j = 0; j < N; j++) {
S:      B_exp[i][j] = tmp + 3;
    }
T:  A_exp[i] = B[i];
}

There is no read from A, so the expansion of A is done. There is a read from B in the statement T. At this step, we need the RAW dependences. In our case, statement T depends on statement S because the memory location reads by statement T is written by statetement S during j-loop iterations. The dependency looks like :

\[\{ T[i] \rightarrow S[i][i] : 0\le i \le N \}\]

Now that we know that the statement T must read its value from the statement S at index [i,i], we only have to know the name of the expanded version of B and modify the read. After read expansion, the source code looks like that :

int tmp;
for (int i = 0; i < N; i++) {
    tmp = i;
    for (int j = 0; j < N; j++) {
S:      B_exp[i][j] = tmp + 3;
    }
T:  A_exp[i] = B_exp[i][i];
}

Limitation 1: Read & Write access inside the same statement.

In the following we will describe a small limitation of our current implementation. Let us consider the following example.

for (int i = 0; i < N; i++) {
    for (int j = 0; j < N; j++) {
        B[i] = ... ;
        ... = B[i];
    }
}

Polly will model the two instructions as one ScopStatement and detect two memory access inside this statement :

Read : \(\{ S[i, j] \rightarrow B[i] : 0 \le i \le N, 0 \le j \le N \}\) Write : \(\{ S[i, j] \rightarrow B[i] : 0 \le i \le N, 0 \le j \le N \}\)

Then Polly will give these two memory accesses to ISL. But ISL has no information on the order in which the memory accesses appear so it decide that the read comes first, which is not the case in our example. This is a design decision inside Polly that requires us to bail out if such a case is possible.

Limitation 2: Union map needed as access relation

for (int i = 0; i < N; i++) {
    B[i] = ... ;
    for (int j = 0; j < N; j++) {
        B[j] = ... ;
    }
    ... = B[i];
}

The only-write expanded version of this example would look like this :

for (int i = 0; i < N; i++) {
    B_exp[i] = ... ;
    for (int j = o; j < M; j++) {
        B_exp2[i][j] = ... ;
    }
    ... = B[i+2];
}

To read of B can read either from B_exp or from B_exp2. Its memory access relation would look like, assuming that $N>M$ :

\[\{ T[i] \rightarrow B\_exp[i] : i \ge M, 0 \le i \le N, 0 \le j \le M \ ; T[i] \rightarrow B\_exp2[i][i] : i < M, 0 \le i \le N, 0 \le j \le M \}\]

Limitation 3: Copy-In & Copy-Out

For accesses that have been initialized outside the loop where we have our read statements, we need to be able to copy in any data that would have been read from the outside. Let us consider the following example:

for (int i = 0; i < N; i++) {
    ... = B[i];
    for (int j = 0; j < N; j++) {
        B[j] = ... ;
    }
}

The expanded version of this example would look like :

for (int i = 0; i < N; i++) {
    ... = B_exp[i][i];
    for (int j = 0; j < N; j++) {
        B_exp[i][j] = ... ;
    }
}

The problem is that nobody is writing $B_exp[i][i]$ before it is reading. So we need a copy in mechanism to manually copy data to $B_exp$ from the original array. This mechanism is not yet implemented. The same problem appears when someone is reading a value expanded outside of the Scop. This is the problem of copy-in/out. For now, we just bail out such cases.

Further bailout-conditions for static expansion

Following our incremental approach we, therefore, preclude our expansion with aggressive filtering of all access patterns that we cannot handle yet (or not at all). This filtering will block the expansion of the memory access, if:

• the associated ScopArrayInfo performs a MayWrite access.
• the associated ScopArrayInfo has more than one MustWrite access, because this would require us to form the union of more than one access and use it as the new access relation of the ScopArrayInfo. This is not supported by Polly for now.
• we would have to read in data from the original array (Copy-In). This is still a work in progress and not yet supported. But nothing inside Polly prevents us in adding support for this.
• we would have to read expanded data after the SCoP (Copy-Out). This is still a work in progress and not yet supported. But nothing inside Polly prevents us in adding support for this.
• we find a read and a write access to the same array inside a single statement. Here we cannot guarantee correctness because of the granularity of statements inside Polly.

Evaluation

Our evaluation considers, for simplicity, only polybench right now. The benchmark suite contains small isolated examples that can directly make use of static expansion to eliminate false dependencies as much as possible (Obviously, this uncovered a few bugs that need to be ironed out as well).

For the evaluation of this project, we have generated a set of patches that add compile-stime statistics. These patches are not yet integrated into Polly as of now, but will be added shortly. These statistics enable us to count the number of accesses we were able to expand and would have been able to expand, if Copy-In/-Out is available. Furthermore, we track the amount of memory that is required in both situations. This gives as a nice estimate about the impact on the memory footprint, if we enable static expansion. This could also be used to implement a threshold for static expansion. A user might then specifiy an upper-bound on the memory-usage per SCoP to control the static expansion (not implemented).

The following charts are generated using pygal4, a Python library to generate charts. Polybench comes with 30 benchmarks. Out of those 30, we are able to compile 22 successfully. Eight crash during compilation, we are investigating the reason for this. For the compile-time comparison we refer to the polybench’s EXTRALARGE_DATASET. For our run-time evaluation we had to use the biggest dataset that fit into the main-memory of the test-machine. This would be LARGE_DATASET for most benchmarks and MEDIUM_DATASET for a few selected ones.

What if we have copy-in/out ?

The idea is to know, for all users of the ScopArrayInfo, if the user is inside or outside the loop in which the write (for MemoryKind::Array and MemoryKind::Value) or the read (for MemoryKind::PHI) happened.

To proove the necessity of copy-in/out implementation, we compare the number of expandable memory accesses than are expanded now and the one that would be expandable if we would have copy-in/out.

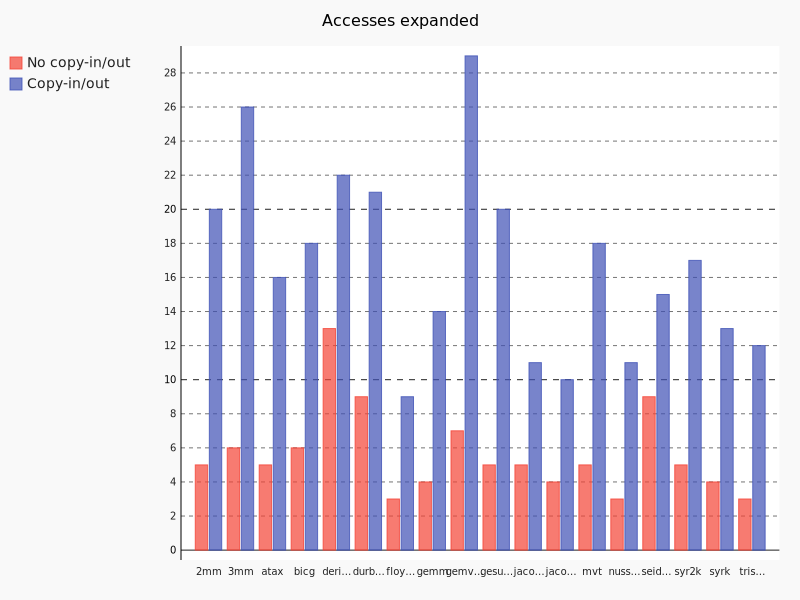
We clearly see with this chart that, if the copy-in/out would have been implemented, way more memory accesses would have been expanded. But expanding more memory accesses can lead to memory space problems. Let us look at the impact of static expansion on the memory needed to store the expanded arrays.

Memory usage

Obviously, static expansion can increase the memory usage quite a lot. What sounds bad at first, is actually a success for us. Because an increase in memory usage shows that we actually expanded acceesses. At the same time we trade this memory for the elimination of dependencies, which in turn enables parallelization. Again, for both Copy-In/-Out available and not available we compare the memory usage for the expansion.

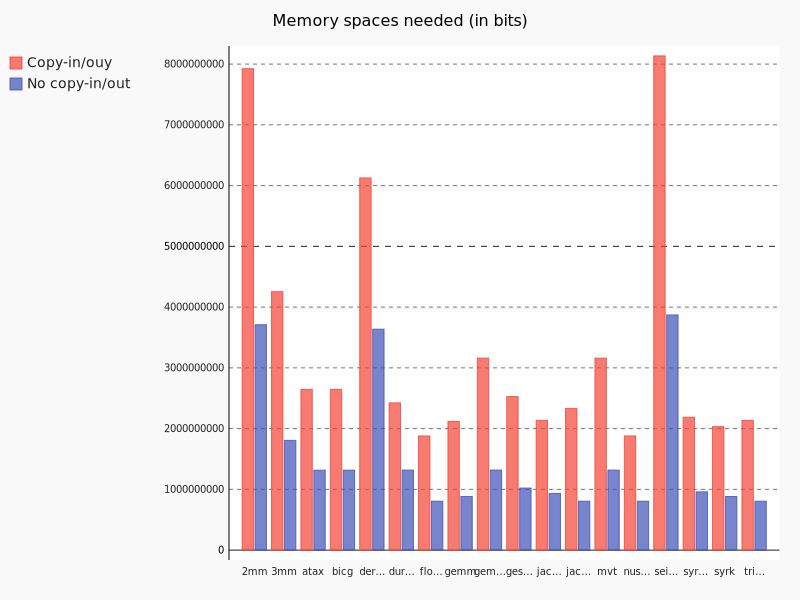
The memory needed for array allocation is huge. For example, for 2mm without copy-in/out, with the EXTRALARGE_DATASET of polybench, we need more than 327Mb. If copy-in/out would have been in place, the ammount of space needed would be very large. Even if the current memory available on machines is huge, the need of a way to select which SAI to expand and also a way to expand in an efficient manner (Maximal Static Expansion) is felt.

Runtime Evaluation

We close up the evaluation with an overview over the execution behavior of our static expansion implementation. At first, we look at the overall increase in memory consumption, measured with UNIX’s implementation of /usr/bin/time. This gives us access to the maximum resident size (RSS). Without any filtering we see a comparison between the baseline (-O3) and clang with static expansion enabled (MSE) enabled. For these experiments, we explicitly disabled operand-tree optimizaion and DeLICM to get an isolated view on only our transformation.

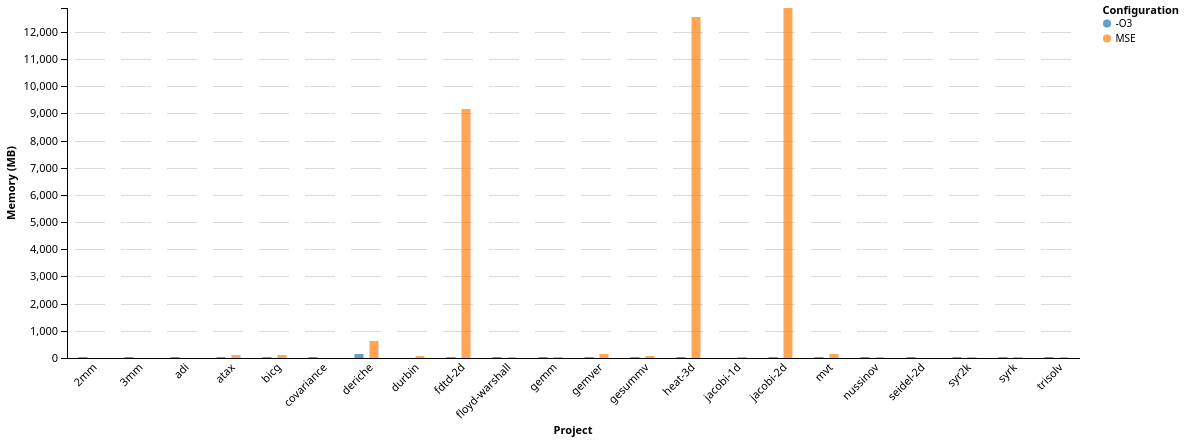
We can directly see the extreme increase in memory consumption when looking at the benchmarks ‘fdtd-2d’, ‘heat-3d’, ‘jacobi-2d’. If we look at memory consumption values lower than 200MB, we can get a more detailed view on the remaining benchmarks:

As expected, whenever we are able to expand accesses, we increase the amount of memory consumed by the benchmark. We also can see the benchmarks where we were not able to finish compilation/execution, either because of bugs in our code, or due to being killed by the systems OOM-Killer process (we reserved too much memory for the system to handle). Finally, without any schedule optimization enabled in Polly, we did not expect to be able to gain speedup by just expanding memory accesses. However, due to the reduction in dependencies, we already enable transformations in the Polly optimization pipeline, e.g., tiling.

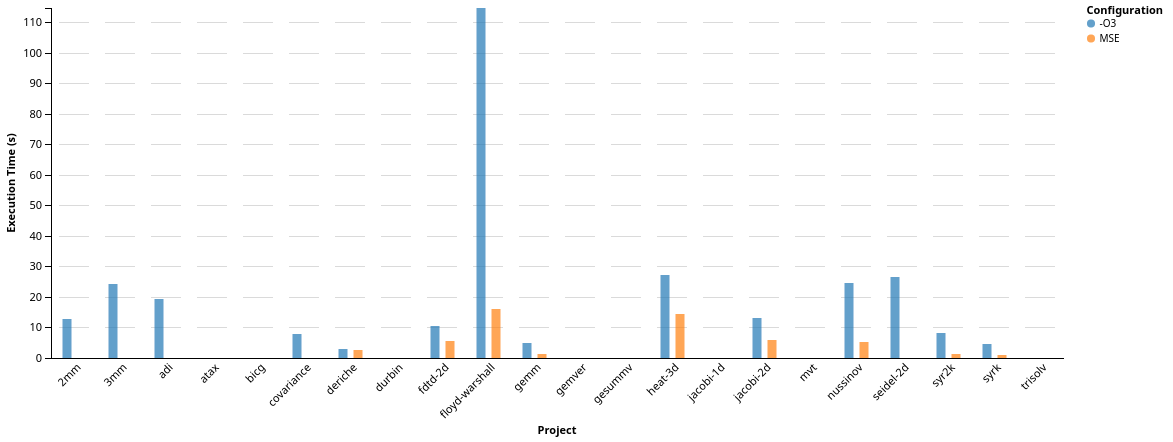
Interestingly, the benchmarks ‘floyd-warshal’, ‘nussinov’, did not suffer from memory consumption increase, although we were able to expand accesses at compile-time. This suggests that by expanding an already fully-dimensional access we were able to change the memory access pattern in a positive way. A missing orange bar means that the benchmark crashed at run-time either because of a bug in our expansion, or because of too much memory being consumed. These will be resolved in the next weeks.

Future Work

Unfortunately, due to lake of time, a few desireable features have not been implemented yet, but will be completed in a few weeks.

• As we see before, a copy-in/out mechanism is crucial. This is the next step. Our evaluation already shows that this would greatly increase the applicability.
• For now, the expansion is only a Fully-indexed one, which is obviously not the most efficient way to expand memory accesses. The next step would be to implement the expansion described in the paper mentionned in introduction.
• For now, we expand all ScopArrayInfo, which is obviously not a good idea. Some of them probably lead to a less efficient code when expanded. A way to select which ScopArrayInfo to expand must be implemented.

References

Static Expansion. Int. J. Parallel Program. 28, 3 (June 2000), 213-243. DOI=http://dx.doi.org/10.1023/A:1007500431910

international conference on Supercomputing (ICS ‘88), J. Lenfant (Ed.). ACM, New York, NY, USA, 429-441. DOI=http://dx.doi.org/10.1145/55364.55406

at: http://www.elis.ugent.be/aces/edegem2002/vanbroekhoven.pdf [Accessed 22 Aug. 2017].

Appendix: Implementation details

The method $expandWrite$ is pretty simple. As its name suggests, the aim of this method is to expand write access. Here is a textual description of the algorithm.

Get the current access relation map.

  // Get domain from the current AM.
  auto Domain = CurrentAccessMap.domain();

Add output dimensions according to the loop nest.

  unsigned in_dimensions = CurrentAccessMap.dim(isl::dim::in);

  // Add dimensions to the new AM according to the current in_dim.
  NewAccessMap = NewAccessMap.add_dims(isl::dim::out, in_dimensions);

Get or Create the expanded ScopArrayInfo.

 // Create the string representing the name of the new SAI.
  // One new SAI for each statement so that each write go to a different memory
  // cell.
  auto CurrentStmtDomain = MA->getStatement()->getDomain();
  auto CurrentStmtName = CurrentStmtDomain.get_tuple_name();
  auto CurrentOutId = CurrentAccessMap.get_tuple_id(isl::dim::out);
  std::string CurrentOutIdString =
      MA->getScopArrayInfo()->getName() + "_" + CurrentStmtName + "_expanded";

  // Create the size vector.
  std::vector<unsigned> Sizes;
  for (unsigned i = 0; i < in_dimensions; i++) {
    assert(isDimBoundedByConstant(CurrentStmtDomain, i) &&
           "Domain boundary are not constant.");
    auto UpperBound = getConstant(CurrentStmtDomain.dim_max(i), true, false);
    assert(!UpperBound.is_null() && UpperBound.is_pos() &&
           !UpperBound.is_nan() &&
           "The upper bound is not a positive integer.");
    assert(UpperBound.le(isl::val(CurrentAccessMap.get_ctx(),
                                  std::numeric_limits<int>::max() - 1)) &&
           "The upper bound overflow a int.");
    Sizes.push_back(UpperBound.get_num_si() + 1);
  }

  // Get the ElementType of the current SAI.
  auto ElementType = MA->getLatestScopArrayInfo()->getElementType();

  // Create (or get if already existing) the new expanded SAI.
  auto ExpandedSAI =
      S.createScopArrayInfo(ElementType, CurrentOutIdString, Sizes);
  ExpandedSAI->setIsOnHeap(true);

Set the out tuple id.

  // Set the out id of the new AM to the new SAI id.
  NewAccessMap = NewAccessMap.set_tuple_id(isl::dim::out, NewOutId);

Add constraints to link input and ouput variables.

  // Add constraints to linked output with input id.
  auto SpaceMap = NewAccessMap.get_space();
  auto ConstraintBasicMap =
      isl::basic_map::equal(SpaceMap, SpaceMap.dim(isl::dim::in));
  NewAccessMap = isl::map(ConstraintBasicMap);

Set the new access relation to the memory access.

  // Set the new access relation map.
  MA->setNewAccessRelation(NewAccessMap);

We return the expanded ScopArrayInfo for the sake of simplicity because we will need it in the $expandRead$ method. Here is the full code of $expandWrite$ method :

ScopArrayInfo *MaximalStaticExpander::expandWrite(Scop &S, MemoryAccess *MA) {

  // Get the current AM.
  auto CurrentAccessMap = MA->getAccessRelation();

  unsigned in_dimensions = CurrentAccessMap.dim(isl::dim::in);

  // Get domain from the current AM.
  auto Domain = CurrentAccessMap.domain();

  // Create a new AM from the domain.
  auto NewAccessMap = isl::map::from_domain(Domain);

  // Add dimensions to the new AM according to the current in_dim.
  NewAccessMap = NewAccessMap.add_dims(isl::dim::out, in_dimensions);

  // Create the string representing the name of the new SAI.
  // One new SAI for each statement so that each write go to a different memory
  // cell.
  auto CurrentStmtDomain = MA->getStatement()->getDomain();
  auto CurrentStmtName = CurrentStmtDomain.get_tuple_name();
  auto CurrentOutId = CurrentAccessMap.get_tuple_id(isl::dim::out);
  std::string CurrentOutIdString =
      MA->getScopArrayInfo()->getName() + "_" + CurrentStmtName + "_expanded";

  // Set the tuple id for the out dimension.
  NewAccessMap = NewAccessMap.set_tuple_id(isl::dim::out, CurrentOutId);

  // Create the size vector.
  std::vector<unsigned> Sizes;
  for (unsigned i = 0; i < in_dimensions; i++) {
    assert(isDimBoundedByConstant(CurrentStmtDomain, i) &&
           "Domain boundary are not constant.");
    auto UpperBound = getConstant(CurrentStmtDomain.dim_max(i), true, false);
    assert(!UpperBound.is_null() && UpperBound.is_pos() &&
           !UpperBound.is_nan() &&
           "The upper bound is not a positive integer.");
    assert(UpperBound.le(isl::val(CurrentAccessMap.get_ctx(),
                                  std::numeric_limits<int>::max() - 1)) &&
           "The upper bound overflow a int.");
    Sizes.push_back(UpperBound.get_num_si() + 1);
  }

  // Get the ElementType of the current SAI.
  auto ElementType = MA->getLatestScopArrayInfo()->getElementType();

  // Create (or get if already existing) the new expanded SAI.
  auto ExpandedSAI =
      S.createScopArrayInfo(ElementType, CurrentOutIdString, Sizes);
  ExpandedSAI->setIsOnHeap(true);

  // Get the out Id of the expanded Array.
  auto NewOutId = ExpandedSAI->getBasePtrId();

  // Set the out id of the new AM to the new SAI id.
  NewAccessMap = NewAccessMap.set_tuple_id(isl::dim::out, NewOutId);

  // Add constraints to linked output with input id.
  auto SpaceMap = NewAccessMap.get_space();
  auto ConstraintBasicMap =
      isl::basic_map::equal(SpaceMap, SpaceMap.dim(isl::dim::in));
  NewAccessMap = isl::map(ConstraintBasicMap);

  // Set the new access relation map.
  MA->setNewAccessRelation(NewAccessMap);

  return ExpandedSAI;
}

As its name suggests, the $expandRead$ method expand the read access passed in parameter. The algorithm is pretty simple too. The goal is to map the read to the last write to the array involved.

First, we get the RAW dependences relevant for the read.

  // Get RAW dependences for the current WA.
  auto WriteDomainSet = MA->getAccessRelation().domain();
  auto WriteDomain = isl::union_set(WriteDomainSet);

  // Get the dependences relevant for this MA
  auto MapDependences = filterDependences(S, Dependences, MA);

  // If no dependences, no need to modify anything.
  if (MapDependences.is_empty())
    return;


  assert(isl_union_map_n_map(MapDependences.get()) == 1 &&
         "There are more than one RAW dependencies in the union map.");
  auto NewAccessMap = isl::map::from_union_map(MapDependences);

The $filterDependences$ method filters the relevant dependences.

Then we set the out id of the map with the id of the expanded array.

  auto Id = ExpandedSAI->getBasePtrId();

  // Replace the out tuple id with the one of the access array.
  NewAccessMap = NewAccessMap.set_tuple_id(isl::dim::out, Id);

At the end, we set the new access relation to the memory access.

  // Set the new access relation.
  MA->setNewAccessRelation(NewAccessMap);

Here is the full version of $expandRead$ :

void MaximalStaticExpander::expandRead(Scop &S, MemoryAccess *MA,
                                       const isl::union_map &Dependences,
                                       ScopArrayInfo *ExpandedSAI) {

  // Get the current AM.
  auto CurrentAccessMap = MA->getAccessRelation();

  // Get RAW dependences for the current WA.
  auto WriteDomainSet = MA->getAccessRelation().domain();
  auto WriteDomain = isl::union_set(WriteDomainSet);

  // Get the dependences relevant for this MA
  auto MapDependences = filterDependences(S, Dependences, MA);

  // If no dependences, no need to modify anything.
  if (MapDependences.is_empty())
    return;


  assert(isl_union_map_n_map(MapDependences.get()) == 1 &&
         "There are more than one RAW dependencies in the union map.");
  auto NewAccessMap = isl::map::from_union_map(MapDependences);

  auto Id = ExpandedSAI->getBasePtrId();

  // Replace the out tuple id with the one of the access array.
  NewAccessMap = NewAccessMap.set_tuple_id(isl::dim::out, Id);

  // Set the new access relation.
  MA->setNewAccessRelation(NewAccessMap);
}